Old Bayesian Seasoning
Simple conversations become nuanced and insightful with a sprinkling of conditional probability.
Bayes' rule is simple. It looks like this:
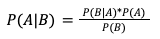
If your eyes glazed over in your last statistics class, we can say this as a sentence:
“The probability of A, if B is true…is equal to the probability of B, if A is true, multiplied by the probability of A, divided by the probability of B.”1
The math is equally simple - multiplication and division only. And even though we mastered these ideas before exiting elementary school, somehow, the implication of this theorem still leaves society dumbfounded.
EXAMPLE #1
Let’s play a game. All statistics are mostly, but not entirely fictitious.
P(A) = Odds that someone in California is employed full-time and works in tech.
P(B) = Odds that someone in California has a net worth in excess of $10M.
P(B|A) = Odds of having a net worth in excess of $10M, given that they’re at a startup
P(A)=0.13 2
P(B)=0.015 3
P(B|A)= 0.05 4
So now, using Bayes' theorem we can calculate P(A|B), which in English is “the odds that someone works at a tech startup, given that they’re worth $10M+.”
This math is easy:
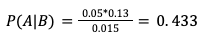
Bayes says (or I say using his theorem?) that 43.3% of the $10M+ net worth crowd in California work at startups. Now this is where it gets interesting. Most millionaires are over 65.5 This is even more pronounced for billionaires.6 So what if we were to assume that 40% of all the $10M+ folks are retired. That would mean only 60% are actually of working age.
43.3%/60% = ~72%.
So, when you meet a really rich person in California who isn’t over 65, there’s an extremely good chance that they’re in tech.
Does that mean that if you work in tech, you’re extremely likely to build $10M+ in net worth?
Of course not. We already have that number, 5%, which is charitable.
Bayes theorem distinguishes between what we see (most of the working age $10M+ crowd in Cali are in tech) from what is true (most tech people, even in Cali aren’t going to amass that level of wealth). Bayes is a cruel master.
1
This skirts some more esoteric discussions of conditions and independence. You’re welcome.
2
California has ~1.9M tech employees, in a state with a population of ~40M. Let’s say ~20M are of working age and ~15M are employed full-time. 1.9M/15M ~0.13.
3
A household net worth of ~$11M places a family in the top 1%. But folks in California are a little wealthier on average than the U.S. in general, so we’ll make this 1.5%.
4
10% of startups exit, most do not produce $10M wealth, but then, one can probably work at a handful of startups during one’s career, so maybe a 5% chance of catching lightning in a bottle or working for a FAANG company for a couple decades and investing well during a ~30yr period seems defensible (if a little optimistic)?
5
One article suggests that 38% of US millionaires are over 65.
6
The proportion of billionaires over 65 is even higher (at least 40-45%).
EXAMPLE #2
Again, all statistics are mostly, but not entirely fictitious. Let's talk about old people.
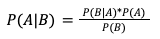
P(A) = Odds that a human being was born in Japan
P(B) = Odds that a human being is alive, and over 112 years old.
P(B|A) = Odds that a human being is alive and over 112, given that they were born in Japan
P(A)=0.016 7
P(B)=5.75*10-9 8
P(B|A)= 1.28*10-7 9
Again, using Bayes' theorem we can calculate P(A|B), which in English is “the odds that someone was born in Japan, given that they are alive and over the age of 112.”
This math is easy:
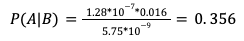
This means that if you meet someone over 112, there should be better than a 1 in 3 chance that they reside in Japan. The empirical data suggest this is true!10 Does this mean that someone born in Japan is remotely likely to live to be 112? Heck no. The odds suggest that only a handful per billion births yield a supercentenarian of this ilk.
Or, to pervert the language of the world’s most interesting man. “Most people don’t live to be 112, but when they do, they’re often from Japan.”
7
The population of Japan is ~125M. There are ~8B people in the world. Simple enough. (And yes, I realize those proportions might be different historically when many of those 8B people were born, and yes, people can immigrate or emigrate, blah blah blah…)
8
There are 46 people currently living, over 112. Again, simple division, see point above.
9
Using the same wikipedia page linked above, there are 16 people residing in Japan currently over the age of 112 (among a population of 125M).
10
Using the same wikipedia page, 16 of the 46 living persons over 112 reside in Japan. That’s ~35%.
EXAMPLE #3
Once more, with feeling. All statistics are mostly, but not entirely fictitious.
Now let’s try the type of example that will inevitably engender vitriol, controversy, and general gnashing of teeth:
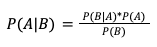
P(A) = Odds that an American is unvaccinated
P(B) = Odds that an American died of COVID-19 between 4/4/2021 and 12/25/2021
P(B|A) = Odds that an American has died of COVID-19, given that they are unvaccinated
P(A)=0.23 11
P(B)=0.00036 12
P(B|A)= 0.00126 13
In english, P(A|B) means “the probability that an American is unvaccinated, given that they died of COVID-19 between April 4th and Christmas of 2021.”
The math is easy:
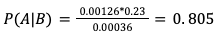
The result above, and the individual terms, imply two points:
- COVID-19 is not that dangerous, even to the unvaccinated.
- The vast majority (80%+) of COVID-19 deaths after vaccinations became available were to unvaccinated individuals. Therefore, if someone passed of COVID in that latter part of 2021, a lack of vaccination was a likely driver, and thus, vaccines saved many lives.
11
US vaccination rate is currently around 77%, according to the Mayo Clinic.
12
According to the CDC, ~117K have perished from COVID-19 in a country of ~330M.
13
Just under 95K in a population of ~330M, 23% of which (~75M), according to the same CDC site linked above.
These types of thought experiments are illustrative, informative, and good exercises for one's reasoning (and they're fun!). For the intrepid reader, consider the following thought experiments:
What is the probability of a human being between the ages of 20 and 40 receiving paychecks from the NBA, given that they are at least 7 feet tall? How does the probability of an NBA player being of caucasian ancestry differ between the subset of players above and below 7 feet in height?
What is the probability of a human being committing suicide (dark, I realize)? How does that probability vary, given that the individual has recently won the lottery?14
What is the probability of becoming president, given that you have attended Harvard, Yale, or Princeton as an undergraduate or a law student? (Since, notably, 15 presidents did!).
14
https://pubmed.ncbi.nlm.nih.gov/29135442/
No one works with an agency just because they have a clever blog. To work with my colleagues, who spend their days developing software that turns your MVP into an IPO, rather than writing blog posts, click here (Then you can spend your time reading our content from your yacht / pied-a-terre). If you can’t afford to build an app, you can always learn how to succeed in tech by reading other essays.
Old Bayesian Seasoning
Simple conversations become nuanced and insightful with a sprinkling of conditional probability.
Bayes' rule is simple. It looks like this:
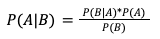
If your eyes glazed over in your last statistics class, we can say this as a sentence:
“The probability of A, if B is true…is equal to the probability of B, if A is true, multiplied by the probability of A, divided by the probability of B.”1
The math is equally simple - multiplication and division only. And even though we mastered these ideas before exiting elementary school, somehow, the implication of this theorem still leaves society dumbfounded.
EXAMPLE #1
Let’s play a game. All statistics are mostly, but not entirely fictitious.
P(A) = Odds that someone in California is employed full-time and works in tech.
P(B) = Odds that someone in California has a net worth in excess of $10M.
P(B|A) = Odds of having a net worth in excess of $10M, given that they’re at a startup
P(A)=0.13 2
P(B)=0.015 3
P(B|A)= 0.05 4
So now, using Bayes' theorem we can calculate P(A|B), which in English is “the odds that someone works at a tech startup, given that they’re worth $10M+.”
This math is easy:
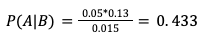
Bayes says (or I say using his theorem?) that 43.3% of the $10M+ net worth crowd in California work at startups. Now this is where it gets interesting. Most millionaires are over 65.5 This is even more pronounced for billionaires.6 So what if we were to assume that 40% of all the $10M+ folks are retired. That would mean only 60% are actually of working age.
43.3%/60% = ~72%.
So, when you meet a really rich person in California who isn’t over 65, there’s an extremely good chance that they’re in tech.
Does that mean that if you work in tech, you’re extremely likely to build $10M+ in net worth?
Of course not. We already have that number, 5%, which is charitable.
Bayes theorem distinguishes between what we see (most of the working age $10M+ crowd in Cali are in tech) from what is true (most tech people, even in Cali aren’t going to amass that level of wealth). Bayes is a cruel master.
1
This skirts some more esoteric discussions of conditions and independence. You’re welcome.
2
California has ~1.9M tech employees, in a state with a population of ~40M. Let’s say ~20M are of working age and ~15M are employed full-time. 1.9M/15M ~0.13.
3
A household net worth of ~$11M places a family in the top 1%. But folks in California are a little wealthier on average than the U.S. in general, so we’ll make this 1.5%.
4
10% of startups exit, most do not produce $10M wealth, but then, one can probably work at a handful of startups during one’s career, so maybe a 5% chance of catching lightning in a bottle or working for a FAANG company for a couple decades and investing well during a ~30yr period seems defensible (if a little optimistic)?
5
One article suggests that 38% of US millionaires are over 65.
6
The proportion of billionaires over 65 is even higher (at least 40-45%).
EXAMPLE #2
Again, all statistics are mostly, but not entirely fictitious. Let's talk about old people.
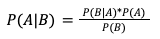
P(A) = Odds that a human being was born in Japan
P(B) = Odds that a human being is alive, and over 112 years old.
P(B|A) = Odds that a human being is alive and over 112, given that they were born in Japan
P(A)=0.016 7
P(B)=5.75*10-9 8
P(B|A)= 1.28*10-7 9
Again, using Bayes' theorem we can calculate P(A|B), which in English is “the odds that someone was born in Japan, given that they are alive and over the age of 112.”
This math is easy:
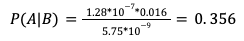
This means that if you meet someone over 112, there should be better than a 1 in 3 chance that they reside in Japan. The empirical data suggest this is true!10 Does this mean that someone born in Japan is remotely likely to live to be 112? Heck no. The odds suggest that only a handful per billion births yield a supercentenarian of this ilk.
Or, to pervert the language of the world’s most interesting man. “Most people don’t live to be 112, but when they do, they’re often from Japan.”
7
The population of Japan is ~125M. There are ~8B people in the world. Simple enough. (And yes, I realize those proportions might be different historically when many of those 8B people were born, and yes, people can immigrate or emigrate, blah blah blah…)
8
There are 46 people currently living, over 112. Again, simple division, see point above.
9
Using the same wikipedia page linked above, there are 16 people residing in Japan currently over the age of 112 (among a population of 125M).
10
Using the same wikipedia page, 16 of the 46 living persons over 112 reside in Japan. That’s ~35%.
EXAMPLE #3
Once more, with feeling. All statistics are mostly, but not entirely fictitious.
Now let’s try the type of example that will inevitably engender vitriol, controversy, and general gnashing of teeth:
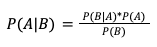
P(A) = Odds that an American is unvaccinated
P(B) = Odds that an American died of COVID-19 between 4/4/2021 and 12/25/2021
P(B|A) = Odds that an American has died of COVID-19, given that they are unvaccinated
P(A)=0.23 11
P(B)=0.00036 12
P(B|A)= 0.00126 13
In english, P(A|B) means “the probability that an American is unvaccinated, given that they died of COVID-19 between April 4th and Christmas of 2021.”
The math is easy:
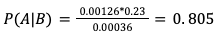
The result above, and the individual terms, imply two points:
- COVID-19 is not that dangerous, even to the unvaccinated.
- The vast majority (80%+) of COVID-19 deaths after vaccinations became available were to unvaccinated individuals. Therefore, if someone passed of COVID in that latter part of 2021, a lack of vaccination was a likely driver, and thus, vaccines saved many lives.
11
US vaccination rate is currently around 77%, according to the Mayo Clinic.
12
According to the CDC, ~117K have perished from COVID-19 in a country of ~330M.
13
Just under 95K in a population of ~330M, 23% of which (~75M), according to the same CDC site linked above.
These types of thought experiments are illustrative, informative, and good exercises for one's reasoning (and they're fun!). For the intrepid reader, consider the following thought experiments:
What is the probability of a human being between the ages of 20 and 40 receiving paychecks from the NBA, given that they are at least 7 feet tall? How does the probability of an NBA player being of caucasian ancestry differ between the subset of players above and below 7 feet in height?
What is the probability of a human being committing suicide (dark, I realize)? How does that probability vary, given that the individual has recently won the lottery?14
What is the probability of becoming president, given that you have attended Harvard, Yale, or Princeton as an undergraduate or a law student? (Since, notably, 15 presidents did!).
14
https://pubmed.ncbi.nlm.nih.gov/29135442/
