BCI: Cars, Statistics, and Neural Latents
Understanding AE's neuroscience machine learning efforts in simpler terms
The human brain is the most complex organization of matter in the known universe. With 80 billion neurons, each sporting ~1000 synapses, modeling the brain would require trillions of variables whose values change rapidly. Current technology allows scientists to measure, at best, the individual activity of thousands of neurons. This leaves a chasm between what can be measured and what must be estimated.1
The good news is that humans are wholly capable of understanding the words spoken by another human being, interpreting their body language, and engaging in complex interaction patterns without ever grasping the details of another person’s neurological data. So if this can be done, then clearly, latent patterns must exist, and something like body language represents an emergent property of latent patterns within those trillions of neurological variables.
But humans are good at this as a result of billions of years of complex evolutionary processes. No neural network, regardless of its sophistication and the number of GPUs deployed for training, has come close… yet. The bleeding edge of machine learning software development for brain computer interface (BCI) technology attempts what other scientific disciplines have attempted for centuries–measure parts of a complex whole, then interpret the patterns that describe the state of the system.
What does this look like in practical terms? What are we actually doing day-to-day to solve these unfathomably complex mathematical challenges? Let’s discuss. We’ll introduce a few quantitative ideas, but ideally, avoid the eyes-glazing-over experience of one’s college statistics class. If nothing else, the topic is a bit more compelling, since we’re ultimately discussing the nature of interaction, understanding, consciousness, and the totality of the human experience.2
Since picturing the electrical activity of neurons or metabolic activity in the brain’s vasculature is beyond the capacities of the human imagination (or at least mine!), let’s consider a complex system with which we engage daily. I reside in Chicago, land of deep dish pizza, Italian beef, and a massive grid of what is currently slush-filled traffic.
We cannot measure the traffic at every intersection in this metropolitan area. Do we need to? Human agency (the ‘A’ in AE) increases when impossibly complex problems are dissected and the pieces turn out to be simpler than imagined.
When I look out my window as I type these words, I observe the frequency at which cars pass. Another way to discuss the same mathematical idea is by measuring the intervals between the arrivals of each car. A simple mathematical structure for describing these intervals is what is called the exponential distribution. It looks like this:

That equation has some ground rules. Firstly, the duration of the interval between cars must be greater than 0 (makes sense, the time between cars arriving cannot be negative). Secondly, there’s only one parameter we need to consider, lambda. A larger lambda means cars arrive more frequently, a smaller lambda means arrivals are more infrequent. Simple.
That simple equation above also has one esoteric, but crucial property. It is said to be memoryless. In other words, the amount of time until the next car arrives does not depend on how long it has been since the last car arrives.3 Whenever I look at my window, the time until the next car shows up is given by the equation above. I don’t need to ask my wife “hey, when did the last car pass the house?”4
Doesn’t seem like much, but it allows us to sum up these intervals. In turn, we can ask, instead of “how long until the next car passes by?” we ask “how many cars will pass by in the next ten minutes?” The sum of samples from an exponential distribution is defined by another mathematical idea, the Poisson Process. It looks like this:
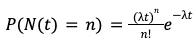
In English, it reads “the probability that n cars pass by in the next t period is some function of that single parameter, lambda.
This is where the magic happens–any location in Chicago (or anywhere else) has some value of that describes it. Busier spots have higher values, quieter service roads have lower values, etc. We could never hope to measure and model all of them. But we don’t need to. You can imagine that, knowing the value of at a few hundred key locations in the greater Chicago area could provide tremendous insight into the traffic at almost any location we could ask for. Suddenly, the rates of cars passing anywhere is, if not precisely known, then at least estimable. And from there, the system can be understood as properties emerge. Perhaps we learn the state in which certain areas are congested and others are flowing freely is consistent with a concert at Wrigley Field or an exodus of disgruntled, frozen Bears fans from Soldier Field after Aaron Rodgers rips out their hearts once again. Perhaps one pattern emerges on Sunday afternoons in the summer when a lakeside highway is closed for bikers. Another emerges at rush hour on a Friday evening. Simple mathematical structures build understanding of a system far beyond the complexity of the equations above.
Now let’s talk about the brain.
The neural latents benchmark challenge (which, at AE, we won!) provides neurological data describing the rate at which particular neurons fire. This is analogous to the parameter describing how often cars pass a given location. The challenge requires machine learning researchers to estimate the firing rate of additional neurons. In terms of the original example, this would be akin to asking, “if I tell you fast cars are passing here, can you estimate how fast cars are passing there?”
Inferring the latent patterns of neural activity from a sparse sampling of neurons is an incredibly important problem. It can unlock the ability to predict and grasp the emergent properties of our brains. The work proceeds by advancing the fundamental neuroscience of how the brain encodes our thoughts, memories, and goals. It leads to a future where we can then decode those same thoughts and goals by measuring the brain’s activity. The possibilities are seemingly limitless. The modeling results of the best research labs in the world have been offered as benchmarks to be surpassed.
This is the first step on a long journey for the human species. We understand the complexity of the cosmos in greater detail than the complexity of the brains that perceive images from telescopes. We understand the topographical nuances of our entire planet in greater detail than topology of the minds that roam its surface.
It’s an unfathomably complex and unimaginably important problem for our species. It begins with simple mathematical ideas.
1
This is a classic example of a “sparse sampling” problem. They emerge in the physical world frequently when the landscape is complex, and sensors are expensive to install and maintain. They emerge when we study a population of human beings, but can inquire in detail about only a comparatively small number. It’s a big deal.
2
Among the greatest sources of suffering for mathematics students is the horribly contrived problem sets with which they grapple repeatedly. No one has ever asked about the moment and location of collision for two trains to any human who has reached the age of majority. Nor has anyone been asked about the probability that three human beings entering a room will have an average height above 6’0’’ unless they’re recruiting basketball players or runway models.
3
P(T > s + t | T > s) = P(T > t). The probability that it takes at least s + t seconds for a car to arrive, given that s seconds have already passed is the same as the probability that it takes at least t seconds for a car to arrive.
4
This is convenient for marital tranquility.
No one works with an agency just because they have a clever blog. To work with my colleagues, who spend their days developing software that turns your MVP into an IPO, rather than writing blog posts, click here (Then you can spend your time reading our content from your yacht / pied-a-terre). If you can’t afford to build an app, you can always learn how to succeed in tech by reading other essays.
BCI: Cars, Statistics, and Neural Latents
Understanding AE's neuroscience machine learning efforts in simpler terms
The human brain is the most complex organization of matter in the known universe. With 80 billion neurons, each sporting ~1000 synapses, modeling the brain would require trillions of variables whose values change rapidly. Current technology allows scientists to measure, at best, the individual activity of thousands of neurons. This leaves a chasm between what can be measured and what must be estimated.1
The good news is that humans are wholly capable of understanding the words spoken by another human being, interpreting their body language, and engaging in complex interaction patterns without ever grasping the details of another person’s neurological data. So if this can be done, then clearly, latent patterns must exist, and something like body language represents an emergent property of latent patterns within those trillions of neurological variables.
But humans are good at this as a result of billions of years of complex evolutionary processes. No neural network, regardless of its sophistication and the number of GPUs deployed for training, has come close… yet. The bleeding edge of machine learning software development for brain computer interface (BCI) technology attempts what other scientific disciplines have attempted for centuries–measure parts of a complex whole, then interpret the patterns that describe the state of the system.
What does this look like in practical terms? What are we actually doing day-to-day to solve these unfathomably complex mathematical challenges? Let’s discuss. We’ll introduce a few quantitative ideas, but ideally, avoid the eyes-glazing-over experience of one’s college statistics class. If nothing else, the topic is a bit more compelling, since we’re ultimately discussing the nature of interaction, understanding, consciousness, and the totality of the human experience.2
Since picturing the electrical activity of neurons or metabolic activity in the brain’s vasculature is beyond the capacities of the human imagination (or at least mine!), let’s consider a complex system with which we engage daily. I reside in Chicago, land of deep dish pizza, Italian beef, and a massive grid of what is currently slush-filled traffic.
We cannot measure the traffic at every intersection in this metropolitan area. Do we need to? Human agency (the ‘A’ in AE) increases when impossibly complex problems are dissected and the pieces turn out to be simpler than imagined.
When I look out my window as I type these words, I observe the frequency at which cars pass. Another way to discuss the same mathematical idea is by measuring the intervals between the arrivals of each car. A simple mathematical structure for describing these intervals is what is called the exponential distribution. It looks like this:

That equation has some ground rules. Firstly, the duration of the interval between cars must be greater than 0 (makes sense, the time between cars arriving cannot be negative). Secondly, there’s only one parameter we need to consider, lambda. A larger lambda means cars arrive more frequently, a smaller lambda means arrivals are more infrequent. Simple.
That simple equation above also has one esoteric, but crucial property. It is said to be memoryless. In other words, the amount of time until the next car arrives does not depend on how long it has been since the last car arrives.3 Whenever I look at my window, the time until the next car shows up is given by the equation above. I don’t need to ask my wife “hey, when did the last car pass the house?”4
Doesn’t seem like much, but it allows us to sum up these intervals. In turn, we can ask, instead of “how long until the next car passes by?” we ask “how many cars will pass by in the next ten minutes?” The sum of samples from an exponential distribution is defined by another mathematical idea, the Poisson Process. It looks like this:
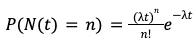
In English, it reads “the probability that n cars pass by in the next t period is some function of that single parameter, lambda.
This is where the magic happens–any location in Chicago (or anywhere else) has some value of that describes it. Busier spots have higher values, quieter service roads have lower values, etc. We could never hope to measure and model all of them. But we don’t need to. You can imagine that, knowing the value of at a few hundred key locations in the greater Chicago area could provide tremendous insight into the traffic at almost any location we could ask for. Suddenly, the rates of cars passing anywhere is, if not precisely known, then at least estimable. And from there, the system can be understood as properties emerge. Perhaps we learn the state in which certain areas are congested and others are flowing freely is consistent with a concert at Wrigley Field or an exodus of disgruntled, frozen Bears fans from Soldier Field after Aaron Rodgers rips out their hearts once again. Perhaps one pattern emerges on Sunday afternoons in the summer when a lakeside highway is closed for bikers. Another emerges at rush hour on a Friday evening. Simple mathematical structures build understanding of a system far beyond the complexity of the equations above.
Now let’s talk about the brain.
The neural latents benchmark challenge (which, at AE, we won!) provides neurological data describing the rate at which particular neurons fire. This is analogous to the parameter describing how often cars pass a given location. The challenge requires machine learning researchers to estimate the firing rate of additional neurons. In terms of the original example, this would be akin to asking, “if I tell you fast cars are passing here, can you estimate how fast cars are passing there?”
Inferring the latent patterns of neural activity from a sparse sampling of neurons is an incredibly important problem. It can unlock the ability to predict and grasp the emergent properties of our brains. The work proceeds by advancing the fundamental neuroscience of how the brain encodes our thoughts, memories, and goals. It leads to a future where we can then decode those same thoughts and goals by measuring the brain’s activity. The possibilities are seemingly limitless. The modeling results of the best research labs in the world have been offered as benchmarks to be surpassed.
This is the first step on a long journey for the human species. We understand the complexity of the cosmos in greater detail than the complexity of the brains that perceive images from telescopes. We understand the topographical nuances of our entire planet in greater detail than topology of the minds that roam its surface.
It’s an unfathomably complex and unimaginably important problem for our species. It begins with simple mathematical ideas.
1
This is a classic example of a “sparse sampling” problem. They emerge in the physical world frequently when the landscape is complex, and sensors are expensive to install and maintain. They emerge when we study a population of human beings, but can inquire in detail about only a comparatively small number. It’s a big deal.
2
Among the greatest sources of suffering for mathematics students is the horribly contrived problem sets with which they grapple repeatedly. No one has ever asked about the moment and location of collision for two trains to any human who has reached the age of majority. Nor has anyone been asked about the probability that three human beings entering a room will have an average height above 6’0’’ unless they’re recruiting basketball players or runway models.
3
P(T > s + t | T > s) = P(T > t). The probability that it takes at least s + t seconds for a car to arrive, given that s seconds have already passed is the same as the probability that it takes at least t seconds for a car to arrive.
4
This is convenient for marital tranquility.
