When Scale Guarantees Failure
Why wishful thinking scales horribly, but is entertaining for baseball fans! (It also might lead to a date with Marilyn Monroe)

In the summer of 1941, a few months before the United States would enter the second world war, the nation’s attention focused upon an Italian-American from California who had made his way to Manhattan. Still two years away from his entering the War, and over a decade away from his tumultuous marriage to Marilyn Monroe, Joltin’ Joe DiMaggio completed a statistical aberration that remains unmatched (even unapproached) over the 80 years since. For 56 consecutive games, DiMaggio achieved at least one base hit. Seems a tad anticlimactic, given the introduction. Don’t most major leaguers manage a hit in most of the games they play? Indeed they do.
And yet, MLB’s Beat the Streak challenge offers a prize north of $5 million USD (*places pinky to the corner of mouth, a la Dr. Evil*) for any individual who can, over the course of 57 days, select 57 players who manage at least one hit in a single game. In other words, on day one, you can select the left-handed singles specialist facing the inept right-handed, bottom-of-the-rotation innings-eater; then on day two, select the league leader in hits playing in the cavernous confines of Coors field in Colorado; and on day three choose another alliteration and a similarly advantageous assignee.

Even with such a generous construct, thousands of players with dozens of attempts apiece haven’t come close to earning the prize. So the good people at the MLB offered a mulligan feature, wherein a streak of between 10 and 15 games can be preserved, even if a player fails to record a hit.
Still, no one has won. It remains, like the lost city of El Dorado, a perfect NCAA tournament bracket, or Ahab’s whale, that which seems tantalizingly close, but forever unattainable. Inevitably, Lucy pulls away the football, the shimmering mirage vanishes into dust, and the sign that reads “free beer tomorrow” reads the same when tomorrow comes. Why is this the case?

The answer lies in the idea that single points of failure are a plague on all our models! If one failure brings down the house then the house is coming down. So what is the probability of a baseball player getting at least one hit in a single ball game?
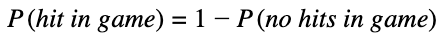
Seems obvious enough, but as it turns out, the probability of a batter failing to record a hit is far easier to calculate. Don’t solve a difficult problem when an easier one achieves the same result.
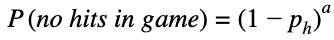
In this case, ph denotes the probability of a batter recording a hit in a given plate appearance, and a represents the number of plate appearances for a batter in a given game. Therefore, the probability of an n-game hitting streak is:

While ph depends on the attributes of the player in question, a is a function of the team on which he plays (better teams have more players reach base, thus increasing the average number of opportunities per game) and the position in the batting order (a leadoff hitter offers a higher a than anyone else on their team).
Yet, much like the economist who estimates the volume of a horse by presuming that it is a sphere, we can offer some simplifying assumptions. First, the value of a is roughly 4.2 in the current MLB (the worst teams are around 4.0 and the best somewhere north of 4.3, and sure, leadoff hitters get a boost, but I digress). And in the modern MLB, where walks and strikeouts are more frequent than at any point in the past century, ph sits around 0.22. This implies that the probability of a player managing a hit in a single game is roughly 0.65, but the odds of a random player earning a hit in 56 consecutive games is approximately 36,000,000,000:1. And of course, to win the grand prize requires a 57-game streak, diminishing the odds to (fittingly) somewhere around 56,000,000,000:1.
How does this inform how AE plans and executes projects? Most software projects, data science modeling exercises, and both startup and enterprise strategies are less egregious in terms of their improbability, but, the lesson remains: If success demands that everything turns out as planned, then success is unlikely.
Joltin’ Joe, however, was hardly an average player. In his fateful 1941 season, he struck out 13 times. There are major leaguers who whiff that frequently in a week and receive nearly seven figures for that interval. DiMaggio is like the finest engineer whose fingers have ever graced a keyboard, crafting the least-buggy software a peer has ever reviewed. To paraphrase the eloquence of Paul Simon, our coders turn their bleary eyes to you (woo woo woo...). What’s that you say, Mrs. Manager? Even Joltin’ Joe leads you astray? (hey hey hey…)

Joe’s ph wasn’t 0.22 in 1941, but ~0.277. And since he found himself ensconced in a lineup that had won four of the last five world series titles (and would win again in 1941), his a wasn’t 4.2, but 5.0. His probability of managing a hit in a given game wasn’t 0.65, but just north of 0.80. And thus, he was more likely to amass a 56-game hitting streak than the average pastoral pastime participant. And his odds of achieving the feat were still worse than 225,000:1 against, and ~280,000:1 against reaching that 57th game.
Just to be clear, the DiMaggio of software engineers does not exist, despite the numerous 10x developers working for AE! And even if, on some ethereal, astral plane, such a deity of coding would represent an entirely unscalable business model. (Imagine hiring such a mythical figure, then telling your recruiters to find another). Oh, and if you are one, and have not already conquered the galaxy (or even if you have), apply here!
Why must we perseverate upon the impossibility of streaks? (Apart from the monetary opportunities in fading those who wager upon them!) The fact is, all too often, strategies, in software and business alike, rely on the presumption that each component of a plan will succeed. Reality suggests such hubris is unwise. So what is the answer?

Systems, schedules, strategies, and software, all must be designed with the expectation that some components will fail. Imagine, for instance, instead of calculating the odds of DiMaggio getting himself a hit in every one of those 56 games, we allow him some leeway? What if, in an act of immense generosity, we allow him to fail once in 56 games. Suddenly, his odds are much more favorable. Why is this? He can fail to record a hit in game 1, game 2, game 10, game 20, game 43, etc!
What if we allow Joe up to n hitless games in 56?
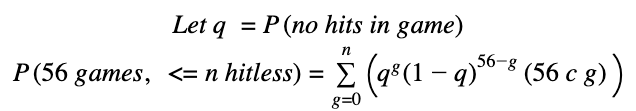
In English, if n=3, we are summing the probabilities of Joe getting a hit in 53 of 56 games, 54 of 56 games, 55 of 56, and all 56. The (56 c g) logic denotes the number of unique combinations of g that are possible in a set of 56[1]. Recalling that the probability of a hit in a game was given by (1-ph)a, we can generalize:
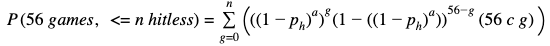
We can visualize the probabilities as n increases, for both Joltin’ Joe’s parameters of ph and a, and for the average Joe.
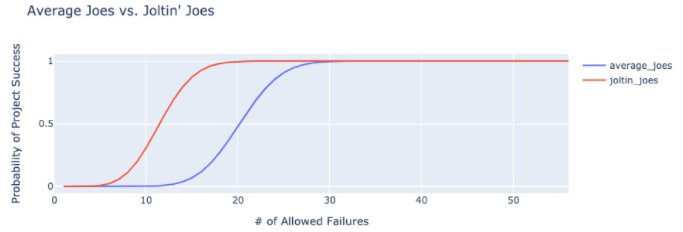
Of course, this is all just an allusion to how we’d approach a project with numerous (56, perhaps?) intermediate steps/objectives/milestones. First, we must choose an acceptable probability that the project succeeds. We resist the urge to spout “100%,” lest a flock (wedge?) of militant black swans descend upon us in a flurry of beaks and excretion. Second, we determine how many of those intermediate goal posts/check-ins/tickets must be completed on-time and as-intended to ensure overall success. Thirdly, we set baselines using a simple mathematical construct–a horizontal line!
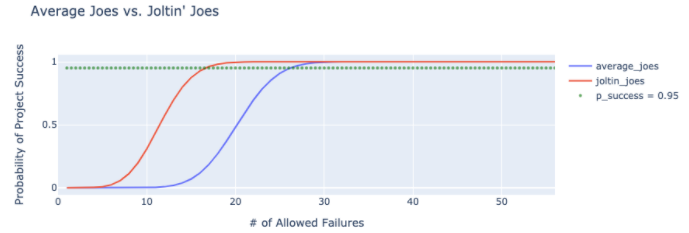
Whether we demand that 95% of our projects succeed or adapt a slightly more swashbuckling attitude and accept 50% success, the same general pattern emerges. In the former case, if our software engineers and project managers are all DiMaggio-level in terms of their aptitude, our project has a 95% chance of success if we allow up to 16 games without a hit, er, tickets-with-bugs/deadlines-extended/meetings-with-stale-danish. If our team is “average joe” level, we’ll need to allow 25-26 oopsies.
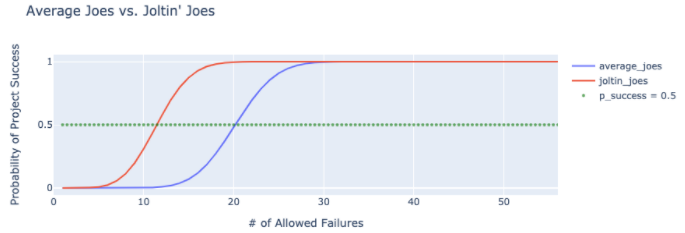
If we only demand a 50% probability of project success, we’ll either need to allow ~11 mishaps to our future hall-of-famers or ~20 to our team of future company softball enthusiasts. And just to flog the deceased equine, what’s easier, Mrs. Manager? Recruiting and hiring a team of DiMaggios or building in the expectation of Mrs. Murphy and her law joining the project?
There are lessons to learn (besides the fact that combinatorics is a fascinating topic):
For one, CEOs crafting next year’s strategic roadmap should play “Beat the Streak,” and recognize that at least some of their best laid plans, be they of mice or men, will go awry. For another, we see the wisdom in Agile project development and sober recognition that when one composes a list of 56 features in scope, even a team led by the Yankee Clipper of coding is going to require some flexibility. This is why AE’s constant over-communication is crucial. And ultimately, with each additional component in a system, we must build in additional latitude for the number of mistakes. Single points of failure do not scale. If a single baseball game with an ace on the mound snaps a hitting streak, then our friends at MLB.com will hold their prize money for years to come.
May your planning be wise and realistic. And may the betting odds be ever in your favor.
1
Back in stats classes of yesteryear, we turned to a triangle named for a French mathematician who likely was born over 1,000 after it first appeared, but had the good fortune of being famous, successful, and Western. I suppose “Pascal’s Triangle” is catchier anyway.
No one works with an agency just because they have a clever blog. To work with my colleagues, who spend their days developing software that turns your MVP into an IPO, rather than writing blog posts, click here (Then you can spend your time reading our content from your yacht / pied-a-terre). If you can’t afford to build an app, you can always learn how to succeed in tech by reading other essays.
When Scale Guarantees Failure
Why wishful thinking scales horribly, but is entertaining for baseball fans! (It also might lead to a date with Marilyn Monroe)

In the summer of 1941, a few months before the United States would enter the second world war, the nation’s attention focused upon an Italian-American from California who had made his way to Manhattan. Still two years away from his entering the War, and over a decade away from his tumultuous marriage to Marilyn Monroe, Joltin’ Joe DiMaggio completed a statistical aberration that remains unmatched (even unapproached) over the 80 years since. For 56 consecutive games, DiMaggio achieved at least one base hit. Seems a tad anticlimactic, given the introduction. Don’t most major leaguers manage a hit in most of the games they play? Indeed they do.
And yet, MLB’s Beat the Streak challenge offers a prize north of $5 million USD (*places pinky to the corner of mouth, a la Dr. Evil*) for any individual who can, over the course of 57 days, select 57 players who manage at least one hit in a single game. In other words, on day one, you can select the left-handed singles specialist facing the inept right-handed, bottom-of-the-rotation innings-eater; then on day two, select the league leader in hits playing in the cavernous confines of Coors field in Colorado; and on day three choose another alliteration and a similarly advantageous assignee.

Even with such a generous construct, thousands of players with dozens of attempts apiece haven’t come close to earning the prize. So the good people at the MLB offered a mulligan feature, wherein a streak of between 10 and 15 games can be preserved, even if a player fails to record a hit.
Still, no one has won. It remains, like the lost city of El Dorado, a perfect NCAA tournament bracket, or Ahab’s whale, that which seems tantalizingly close, but forever unattainable. Inevitably, Lucy pulls away the football, the shimmering mirage vanishes into dust, and the sign that reads “free beer tomorrow” reads the same when tomorrow comes. Why is this the case?

The answer lies in the idea that single points of failure are a plague on all our models! If one failure brings down the house then the house is coming down. So what is the probability of a baseball player getting at least one hit in a single ball game?
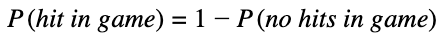
Seems obvious enough, but as it turns out, the probability of a batter failing to record a hit is far easier to calculate. Don’t solve a difficult problem when an easier one achieves the same result.
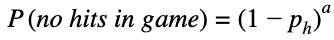
In this case, ph denotes the probability of a batter recording a hit in a given plate appearance, and a represents the number of plate appearances for a batter in a given game. Therefore, the probability of an n-game hitting streak is:

While ph depends on the attributes of the player in question, a is a function of the team on which he plays (better teams have more players reach base, thus increasing the average number of opportunities per game) and the position in the batting order (a leadoff hitter offers a higher a than anyone else on their team).
Yet, much like the economist who estimates the volume of a horse by presuming that it is a sphere, we can offer some simplifying assumptions. First, the value of a is roughly 4.2 in the current MLB (the worst teams are around 4.0 and the best somewhere north of 4.3, and sure, leadoff hitters get a boost, but I digress). And in the modern MLB, where walks and strikeouts are more frequent than at any point in the past century, ph sits around 0.22. This implies that the probability of a player managing a hit in a single game is roughly 0.65, but the odds of a random player earning a hit in 56 consecutive games is approximately 36,000,000,000:1. And of course, to win the grand prize requires a 57-game streak, diminishing the odds to (fittingly) somewhere around 56,000,000,000:1.
How does this inform how AE plans and executes projects? Most software projects, data science modeling exercises, and both startup and enterprise strategies are less egregious in terms of their improbability, but, the lesson remains: If success demands that everything turns out as planned, then success is unlikely.
Joltin’ Joe, however, was hardly an average player. In his fateful 1941 season, he struck out 13 times. There are major leaguers who whiff that frequently in a week and receive nearly seven figures for that interval. DiMaggio is like the finest engineer whose fingers have ever graced a keyboard, crafting the least-buggy software a peer has ever reviewed. To paraphrase the eloquence of Paul Simon, our coders turn their bleary eyes to you (woo woo woo...). What’s that you say, Mrs. Manager? Even Joltin’ Joe leads you astray? (hey hey hey…)

Joe’s ph wasn’t 0.22 in 1941, but ~0.277. And since he found himself ensconced in a lineup that had won four of the last five world series titles (and would win again in 1941), his a wasn’t 4.2, but 5.0. His probability of managing a hit in a given game wasn’t 0.65, but just north of 0.80. And thus, he was more likely to amass a 56-game hitting streak than the average pastoral pastime participant. And his odds of achieving the feat were still worse than 225,000:1 against, and ~280,000:1 against reaching that 57th game.
Just to be clear, the DiMaggio of software engineers does not exist, despite the numerous 10x developers working for AE! And even if, on some ethereal, astral plane, such a deity of coding would represent an entirely unscalable business model. (Imagine hiring such a mythical figure, then telling your recruiters to find another). Oh, and if you are one, and have not already conquered the galaxy (or even if you have), apply here!
Why must we perseverate upon the impossibility of streaks? (Apart from the monetary opportunities in fading those who wager upon them!) The fact is, all too often, strategies, in software and business alike, rely on the presumption that each component of a plan will succeed. Reality suggests such hubris is unwise. So what is the answer?

Systems, schedules, strategies, and software, all must be designed with the expectation that some components will fail. Imagine, for instance, instead of calculating the odds of DiMaggio getting himself a hit in every one of those 56 games, we allow him some leeway? What if, in an act of immense generosity, we allow him to fail once in 56 games. Suddenly, his odds are much more favorable. Why is this? He can fail to record a hit in game 1, game 2, game 10, game 20, game 43, etc!
What if we allow Joe up to n hitless games in 56?
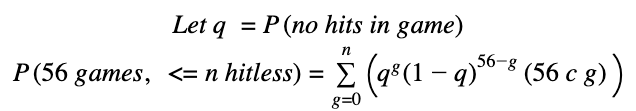
In English, if n=3, we are summing the probabilities of Joe getting a hit in 53 of 56 games, 54 of 56 games, 55 of 56, and all 56. The (56 c g) logic denotes the number of unique combinations of g that are possible in a set of 56[1]. Recalling that the probability of a hit in a game was given by (1-ph)a, we can generalize:
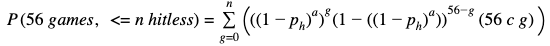
We can visualize the probabilities as n increases, for both Joltin’ Joe’s parameters of ph and a, and for the average Joe.

Of course, this is all just an allusion to how we’d approach a project with numerous (56, perhaps?) intermediate steps/objectives/milestones. First, we must choose an acceptable probability that the project succeeds. We resist the urge to spout “100%,” lest a flock (wedge?) of militant black swans descend upon us in a flurry of beaks and excretion. Second, we determine how many of those intermediate goal posts/check-ins/tickets must be completed on-time and as-intended to ensure overall success. Thirdly, we set baselines using a simple mathematical construct–a horizontal line!

Whether we demand that 95% of our projects succeed or adapt a slightly more swashbuckling attitude and accept 50% success, the same general pattern emerges. In the former case, if our software engineers and project managers are all DiMaggio-level in terms of their aptitude, our project has a 95% chance of success if we allow up to 16 games without a hit, er, tickets-with-bugs/deadlines-extended/meetings-with-stale-danish. If our team is “average joe” level, we’ll need to allow 25-26 oopsies.

If we only demand a 50% probability of project success, we’ll either need to allow ~11 mishaps to our future hall-of-famers or ~20 to our team of future company softball enthusiasts. And just to flog the deceased equine, what’s easier, Mrs. Manager? Recruiting and hiring a team of DiMaggios or building in the expectation of Mrs. Murphy and her law joining the project?
There are lessons to learn (besides the fact that combinatorics is a fascinating topic):
For one, CEOs crafting next year’s strategic roadmap should play “Beat the Streak,” and recognize that at least some of their best laid plans, be they of mice or men, will go awry. For another, we see the wisdom in Agile project development and sober recognition that when one composes a list of 56 features in scope, even a team led by the Yankee Clipper of coding is going to require some flexibility. This is why AE’s constant over-communication is crucial. And ultimately, with each additional component in a system, we must build in additional latitude for the number of mistakes. Single points of failure do not scale. If a single baseball game with an ace on the mound snaps a hitting streak, then our friends at MLB.com will hold their prize money for years to come.
May your planning be wise and realistic. And may the betting odds be ever in your favor.
1
Back in stats classes of yesteryear, we turned to a triangle named for a French mathematician who likely was born over 1,000 after it first appeared, but had the good fortune of being famous, successful, and Western. I suppose “Pascal’s Triangle” is catchier anyway.
