Bugs and Candor
At some point, you're adding bugs faster than you can squash 'em.
TL/DR. You’ll never build every conceivable feature. At some point, we’ll be adding costs in the form of new bugs to squash faster than we’ll be adding value in the form of new features. We can prove this mathematically.
Voltaire once wrote:
Dans ses écrits, un sage Italien
Dit que le mieux est l'ennemi du bien
He was referring to some unnamed, wisened Italian, but the salient point emerges as “the perfect is the enemy of the good.” The aphorism is widely understood, but uniquely poignant for oh-so-many client-facing professionals.
Let us begin to grapple with the wisdom of living nightmares and dead philosophers. Let us explore a simple idea in the language of mathematics and the language of prose. Let us remember why tonsorial damage during witching hours is an inevitable result when we fail to receive the wisdom of Voltaire and little league coaches everywhere1.
Imagine if you will (and I hope you will, it’s lonely if you do not), a project whose completion traverses a statistics professor’s favorite path–the one that begins at 0, ends at 1, and behaves predictably in the middle.
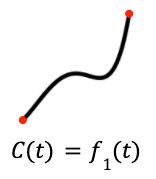
C will denote that 0-to-1 completion amount, as a fraction. Now let us assign some properties to f(t), in calculus and clean English:
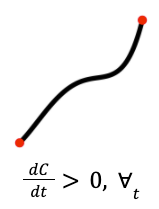
“The completion amount always rises as we invest more time…2”
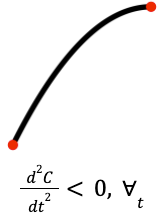
“Each hour is less productive than the last.” (Economics professors use words like “diminishing marginal returns,” corporate operations folks refer to “gathering low-hanging fruit first,” and math teachers might say “concave down”).
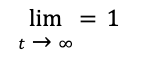
“This project approaches 100% completion, given an infinite amount of time.” (And so help me, if a math professor attacks the semantics of that plain-text description, the limit of my patience will approach 0.”)
Ah, but is life so simple? Is it simply a matter of slowing, but nonetheless inexorable progress towards the desired end? Alas, no. For projects are completed by fallible humans (or software composed by fallible humans), and fallible humans, from time to time, err. Worse, the frequency of these errors does not diminish as time elapses. The most optimistic possible assumption is that f*&k-ups occur linearly with time (spend twice the time, make twice as many mistakes, etc). A more realistic assumption might posit that given the insertion of stress, thrashing, moving goal posts, added complexity, and general team weariness as the project elapses, the rate of errors actually increases with time, but for simplicity and sanity, let’s do this:
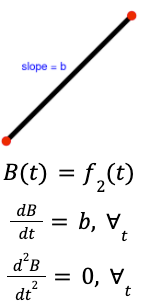
In this case, B is the total amount of time lost in the form of bugs (or other new requirements) created as time passes. The second and third equations essentially say (in mathematical terms), “the rate of new messes to clean up grows at a fixed rate as time goes by–add another week in the kitchen and expect the same amount of spilt milk as the previous week”
Now, let’s add a couple ideas to connect the dots:
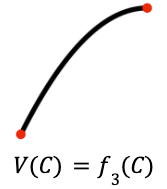
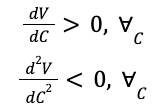
“The value of the project is determined by the amount of all possible features completed. The change in value increases with completion, but with diminishing rates of return.
Finally, for good measure, let’s introduce a stupidly simple, but mission-critical notion. Projects contain a rate for their undertaking, accounting for all personnel, facilities, materials, and caffeine. We’ll call this r, measured as cost per time.
So, where does this leave us?
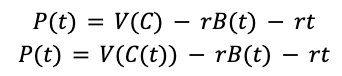
Profits (P) are a function of completeness C, but also of how much time we need to spend building the features (rt) and squashing the bugs we create in our never-ending pursuit of perfection, of completeness, of things about which Voltaire warned us grimly.
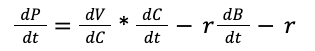
That’s right, there’s a chain rule in there because value is a function of completion and completion is a function of time, and your calculus prof would be so proud of you, or alternatively, wondering why you didn’t pay more attention in class. Either way, we know something about these terms:
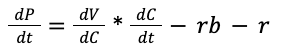
Let’s set dP/dt to 0, and then discuss:
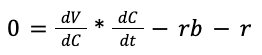
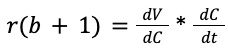
That’s the point of no return, when each additional hour of work creates more costs in terms of the bugs introduced than the value the new features might add. And our assumptions above ‘bout the negative concavity of dV/dC and dC/dt are the nails in our coffins. In other words, we don’t know how much value each new feature adds, but we know that number is falling. We don’t know how much more complete the project will be after another week, but we know that number shrinks too. We don’t know exactly how many bugs we’ll create with each extra week, but that number ain’t falling. Thus, at some point, get the hell out of the kitchen because you’re more likely to spill the roux or burn down the house than make the dish worth more to the diner.
Do we know what that point is when the project begins? Of course not. Do we know, as an immutable mathematical truth, that such a point must exist? Quo Erat Dumbasstradum - the above proves it. Thus, it is incumbent upon us to over-communicate with clients, early and often. First, we must convey, the beginning of any engagement demands better framing. That framing requires the sober realization that some items on the list of all possible features will remain incomplete. Clients and developers must over-communicate to determine scope and make difficult choices. Otherwise, inevitably, the break-even point is going to bite our waiting keesters no matter how robust our undergarments. Secondly, we must over-communicate and discuss as that point approaches so that all parties are prepared to call it a wrap. Thirdly, we must over-communicate regarding what exactly should be assigned highest priority, and what, when the break-even-point’s bell tolls for thee, should be excluded.
The alternative is those final weeks of misery, replete with recriminations, sleep-deprivation, burning piles of cash, and mediocre blog posts.
We give it to our clients straight–perfection doesn’t exist. We won’t waste your time or ours. We will maximize the “good,” slaughtering its aphoristic enemy along the way.
1
My father coached my little league team for years. He would remind children ad infinitum, “the best throw is no throw.” Alternatively, “put the ball in your pocket.” The engineering equivalent might be simply, “an unwritten line of code contains no bugs.”
2
On this theoretical project, we assume there is a finite list of possible features. Even if some of those features are not listed in the initial scoping session, C = 1 means “this project is perfect, containing every conceivable feature, all of which function precisely as desired.” This implies that, as time elapses, we only approach C = 1 (in English, “we never revert features”, in math, “monotonically increasing”). Also, this project emits rainbow and unicorns, vanquishes world hunger, and its feces are olfactorally delightful.
No one works with an agency just because they have a clever blog. To work with my colleagues, who spend their days developing software that turns your MVP into an IPO, rather than writing blog posts, click here (Then you can spend your time reading our content from your yacht / pied-a-terre). If you can’t afford to build an app, you can always learn how to succeed in tech by reading other essays.
Bugs and Candor
At some point, you're adding bugs faster than you can squash 'em.
TL/DR. You’ll never build every conceivable feature. At some point, we’ll be adding costs in the form of new bugs to squash faster than we’ll be adding value in the form of new features. We can prove this mathematically.
Voltaire once wrote:
Dans ses écrits, un sage Italien
Dit que le mieux est l'ennemi du bien
He was referring to some unnamed, wisened Italian, but the salient point emerges as “the perfect is the enemy of the good.” The aphorism is widely understood, but uniquely poignant for oh-so-many client-facing professionals.
Let us begin to grapple with the wisdom of living nightmares and dead philosophers. Let us explore a simple idea in the language of mathematics and the language of prose. Let us remember why tonsorial damage during witching hours is an inevitable result when we fail to receive the wisdom of Voltaire and little league coaches everywhere1.
Imagine if you will (and I hope you will, it’s lonely if you do not), a project whose completion traverses a statistics professor’s favorite path–the one that begins at 0, ends at 1, and behaves predictably in the middle.

C will denote that 0-to-1 completion amount, as a fraction. Now let us assign some properties to f(t), in calculus and clean English:

“The completion amount always rises as we invest more time…2”

“Each hour is less productive than the last.” (Economics professors use words like “diminishing marginal returns,” corporate operations folks refer to “gathering low-hanging fruit first,” and math teachers might say “concave down”).
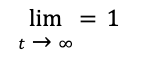
“This project approaches 100% completion, given an infinite amount of time.” (And so help me, if a math professor attacks the semantics of that plain-text description, the limit of my patience will approach 0.”)
Ah, but is life so simple? Is it simply a matter of slowing, but nonetheless inexorable progress towards the desired end? Alas, no. For projects are completed by fallible humans (or software composed by fallible humans), and fallible humans, from time to time, err. Worse, the frequency of these errors does not diminish as time elapses. The most optimistic possible assumption is that f*&k-ups occur linearly with time (spend twice the time, make twice as many mistakes, etc). A more realistic assumption might posit that given the insertion of stress, thrashing, moving goal posts, added complexity, and general team weariness as the project elapses, the rate of errors actually increases with time, but for simplicity and sanity, let’s do this:
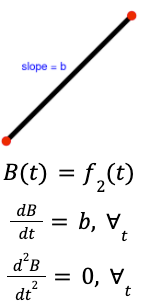
In this case, B is the total amount of time lost in the form of bugs (or other new requirements) created as time passes. The second and third equations essentially say (in mathematical terms), “the rate of new messes to clean up grows at a fixed rate as time goes by–add another week in the kitchen and expect the same amount of spilt milk as the previous week”
Now, let’s add a couple ideas to connect the dots:
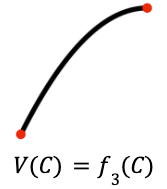
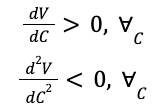
“The value of the project is determined by the amount of all possible features completed. The change in value increases with completion, but with diminishing rates of return.
Finally, for good measure, let’s introduce a stupidly simple, but mission-critical notion. Projects contain a rate for their undertaking, accounting for all personnel, facilities, materials, and caffeine. We’ll call this r, measured as cost per time.
So, where does this leave us?
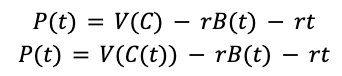
Profits (P) are a function of completeness C, but also of how much time we need to spend building the features (rt) and squashing the bugs we create in our never-ending pursuit of perfection, of completeness, of things about which Voltaire warned us grimly.
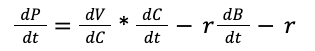
That’s right, there’s a chain rule in there because value is a function of completion and completion is a function of time, and your calculus prof would be so proud of you, or alternatively, wondering why you didn’t pay more attention in class. Either way, we know something about these terms:
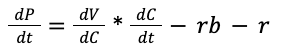
Let’s set dP/dt to 0, and then discuss:
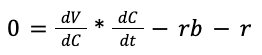
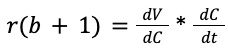
That’s the point of no return, when each additional hour of work creates more costs in terms of the bugs introduced than the value the new features might add. And our assumptions above ‘bout the negative concavity of dV/dC and dC/dt are the nails in our coffins. In other words, we don’t know how much value each new feature adds, but we know that number is falling. We don’t know how much more complete the project will be after another week, but we know that number shrinks too. We don’t know exactly how many bugs we’ll create with each extra week, but that number ain’t falling. Thus, at some point, get the hell out of the kitchen because you’re more likely to spill the roux or burn down the house than make the dish worth more to the diner.
Do we know what that point is when the project begins? Of course not. Do we know, as an immutable mathematical truth, that such a point must exist? Quo Erat Dumbasstradum - the above proves it. Thus, it is incumbent upon us to over-communicate with clients, early and often. First, we must convey, the beginning of any engagement demands better framing. That framing requires the sober realization that some items on the list of all possible features will remain incomplete. Clients and developers must over-communicate to determine scope and make difficult choices. Otherwise, inevitably, the break-even point is going to bite our waiting keesters no matter how robust our undergarments. Secondly, we must over-communicate and discuss as that point approaches so that all parties are prepared to call it a wrap. Thirdly, we must over-communicate regarding what exactly should be assigned highest priority, and what, when the break-even-point’s bell tolls for thee, should be excluded.
The alternative is those final weeks of misery, replete with recriminations, sleep-deprivation, burning piles of cash, and mediocre blog posts.
We give it to our clients straight–perfection doesn’t exist. We won’t waste your time or ours. We will maximize the “good,” slaughtering its aphoristic enemy along the way.
1
My father coached my little league team for years. He would remind children ad infinitum, “the best throw is no throw.” Alternatively, “put the ball in your pocket.” The engineering equivalent might be simply, “an unwritten line of code contains no bugs.”
2
On this theoretical project, we assume there is a finite list of possible features. Even if some of those features are not listed in the initial scoping session, C = 1 means “this project is perfect, containing every conceivable feature, all of which function precisely as desired.” This implies that, as time elapses, we only approach C = 1 (in English, “we never revert features”, in math, “monotonically increasing”). Also, this project emits rainbow and unicorns, vanquishes world hunger, and its feces are olfactorally delightful.
